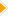西川善司の「試験に出るゲームグラフィックス」（6）レイトレアプローチで作り上げた「The Tomorrow Children」の先進ビジュアル，後編

ジェローム・リアー氏

　長きにわたってレポートしてきた「The Tomorrow Children」編も今回が最終回である。
　従来のゲームグラフィックスの系譜から逸脱した独特なシステムを採用することもあり，前編と中編の難度はかなり高かったと思うが，あらかじめ予告しておくと，今回も負けず劣らず高度な内容になっている。心して読み進めてもらえればと思う。

　なお，今回のテーマは地形システム。メインで解説してもらったのは，キュー・ゲームスで基礎技術研究開発チームのチーフを務めるJerome Liard（ジェローム・リアー，以下カタカナ表記）氏だ。PlayStation（以下，PS）3のユーザーであれば誰もがお世話になったXMBシステムや音楽ビジュアライザの開発にも携わった人物でもある。

西川善司の「試験に出るゲームグラフィックス」（4）レイトレアプローチで作り上げたThe Tomorrow Childrenの先進ビジュアル，前編

西川善司の「試験に出るゲームグラフィックス」（5）レイトレアプローチで作り上げたThe Tomorrow Childrenの先進ビジュアル，中編

The Tomorrow Childrenの3D地形表現を支える技術（1）LDC法

　The Tomorrow Childrenというゲームは，「ゲーム世界に対してプレイヤーが自由に地形を造成できる」という，独特なゲームメカニクスの上に成り立っている。


　これまでにも「ゲーム世界の造成」をテーマにしたゲームは存在する。2D時代であれば「Populous」（ポピュラス，以下カタカナ表記）が代表作ということになるだろう。3Dでも「Populous: The Beginning」（ポピュラス・ザ・ビギニング）などが代表作となりそうだが，いずれにせよ，ほかにも多く存在する“土地造成ゲーム”と同じく，高さ（Height）ベースの土地造成というのが基本線になっていた。
　高さベースの土地造成というのは，あらかじめポリゴン分割しておいた地表に対して高さのデータを与えることで起伏を作り出すものと考えればいい。衛星写真をベースにした山岳地図データも，多くが高さデータを基としたデータ構造になっている。

　それに対してThe Tomorrow Childrenでは，「造成単位」とでも言うべき「土地部品」の単位3Dモデル単位を重ね，積層させていくことで自由な造成を行える。さらに，できあがっている山や造形物に対し，「穴掘り部品」で削岩まで行える仕様にもなっている。
　重要なことは，このような部品（パーツ）単位基準における土地造成と削岩が絡んでくると，高さベースの地形システムでは表現できない点である。空から見た土地の高さ情報だけだと，山に掘ったトンネルを表現しようがないのだ。

　下に示したのは，開発初期のコンセプトアートである。これだけで最終的なゲーム仕様まで推測することはできないものの，それでも，砂場で盛ったり掘ったりするような土地造成コンセプトが存在するのは確認できるだろう。

開発初期のコンセプトアート

　このコンセプトアートはゲームデザイナーによるものだが，開発チームは当初，このコンセプトアートを見たとき，どうすればいいのかと途方に暮れたという。

　自由な地形造成を行えるゲームの代表例としては，「Minecraft」（マインクラフト）がある。Minecraftでは，山を作ることも，穴を掘ってトンネルを掘ることも可能だが，管理はご存じのとおり立方体（ブロック）単位だ。少なくともバニラ状態だと，ライティングもごくごく基本的なものしか適用されていない。
　キュー・ゲームスの代表取締役であるDylan Cuthbert（ディラン・カスバート，以下カタカナ表記）氏によると，The Tomorrow Childrenの場合，Minecraftよりもさらにきめ細かく地形造成を行うゲームにしたかったのだそうだ。

キュー・ゲームスの代表取締役であるカスバート氏。現代ゲーム史の一端を担っていると言っても過言ではない氏の来歴については前編を参照してほしい

カスバート氏：
　The Tomorrow ChildrenはMinecraft的，と言われることがありますが，インスパイアされたゲームを挙げるとすればやはりポピュラスです。
　ただ「同一のゲーム世界を複数のプレイヤーで共有しながら造成を行っていく」というのは，ポピュラスにない要素ですね。
　「動的に造成できて破壊できて，グラフィックスの見た目にも矛盾がないこと」を実現しようとしたら，ここまでユニークなグラフィックシステム，地形システムになってしまったんですよ（笑）。


　ゲームの仕様から，システム仕様としては，

1. 「土地部品」となる3Dモデルをゲーム空間に自由に配置できる。それらは重なり合うことも，常識的な範囲で無数に置いていくことも可能
2. すでに「土地部品」が置いてある空間に対して，同じような「土地部品」で穴を開けていける

という実装になるのは想像できる。では，どう実装するのが最適なのだろう？　地形システムのアーキテクトとして，リアー氏はここに頭を悩ませることになったという。


リア―氏：
　開発の最初期だと，「MeshMixer」（関連リンク）のような，土地部品の3Dモデルを“縫い付けて”いくような実装を試してみましたが，うまくいきません。そこでSigned Distance Field（関連記事）や，ボクセル（Voxel）ベースでの実装も検討しました。
　さまざまな実験を経て決まったのが，「LDC」（Layered Depth Cube，レイヤードデプスキューブ）ベースの実装です。


　上で示した1.の実装だけならともかく，2.まで実装しようとすると，3Dモデル（＝立体物）の論理演算（＝ブーリアン演算）まで配慮しなければならず，とたんに難度が跳ね上がる。複数存在する3Dモデル同士の加算・減算は，いわゆる空間領域構成法（Constructive Solid Geometry，以下 CSG）によるソリッドモデリングそのものである。

立方体（a）と球（b）があったとして，「a＋b」が左下，「a−b」が中央下，「a＊b」（aとbが交わっている部分）が右下になるようモデリングしようという概念が，CSGである

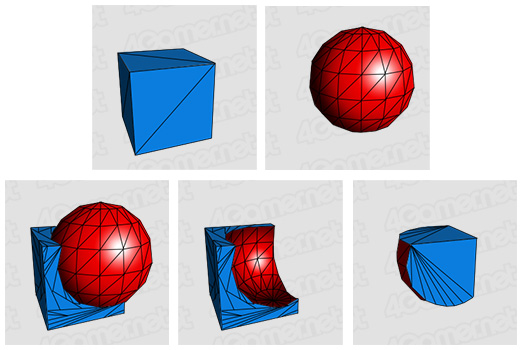　ソリッドモデリング（Solid Modeling）とは，線によるワイヤーフレーム，表面によるサーフェスではなく，中身のある3次元構造として3D立体物を表現する手段のこと。CG技術においてはかなり興味深いテーマの1つだが，そうしたCSGベースのソリッドモデリングを，前編で簡単に取りあげたLDCで実装する方針が，比較的早いタイミングで決定されたというわけだ。


　LDCというキーワード自体の解説も必要だろう。直訳すると「層構造の深度を持った立方体」だが，直訳に囚われないほうが本質を理解しやすい。

　というのもLDCは，一種のポイントクラウド（Point Cloud）的な3Dモデル表現手法だからだ。
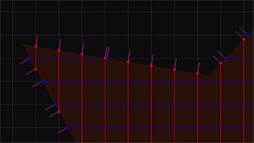
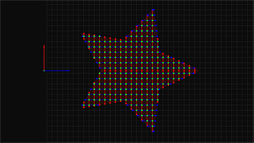
　ポイントクラウドというのは，3D座標を持った点の集合体によって立体物を表現しようというアプローチのこと。LDCの場合は，構成点が任意の3D座標を持つのではなく，立方体状のグリッド（＝ボクセル）を基準にして，X，Y，Zの各軸に平行な線分と，表現対象となる3Dモデルとの境界点の情報を持つようになっている……と，文章で書くと難解だが，下の図を見てもらえば理解できると思う。

左は，星型をした弁当箱のような立体図を真上から見た状態に対し，X軸でスキャンしたときのLDCデータ。「p0」「p1」といった各点は単位グリッドからの距離値で表すことになる。マゼンタ色の線分は法線ベクトル（＝単位界面の向き）を示したものだ。右はカメラの視点を変えてみたところ

同様にY軸方向からもスキャンして得られたLDCデータの一部が，左のスクリーンショットにおける赤い線分だ。右はその状態から“星型弁当箱”全体を表示すべく，カメラを引いて，視点も変えた例

LDCの点情報だけを可視化した例

　あるいは，「X，Y，Zの3軸方向から，単位グリッドにおける一辺の幅で，『何でも通り抜けられるレーザー光線』を表現対象となる3Dモデルに向けて照射し，対象となる3Dモデルのどこにレーザー光が入射し，どこから出射したか，座標のメモを取るイメージ」と言ってもいいかもしれない。この説明に沿って続けるなら，表現対象となる3Dモデルに凹凸がある場合，「入射→出射」のペアが複数になるケースもあるだろう。つまり，基準軸からのLDCデータは固定長ではなく，可変長のポイントリスト構造体ということになる。

X，Y，Zの3軸すべてでスキャンした状態を真上から見たもの（左）と，カメラの角度を変えたもの（右）

　The Tomorrow ChildrenにおけるLDCデータは，基本情報である「単位グリッドの起点からの距離情報と入射（Enter）・出射（Exit）フラグ」だけでなく，後段のグラフィックス描画に深く関わる法線ベクトルや表現材質ID（マテリアルID）も含んだ構成となっている。
　さらにLDCは，2つの3Dモデル同士の論理演算を，非常にシンプルなLDCデータ同士の論理演算に分解できる。2つの3Dモデルの論理加算・減算は，LDCデータ同士の「座標値」（※実際には距離値）の比較と「入射か出射かのフラグ」の判定の組み合わせだけで計算可能なのだ。これはGPUで並列実行するテーマとしても相性がよさそうに思える。
　実際にはLDCデータのメモリレイアウトはあまりGPUにとって都合がよくなかったが，実際にやってみた結果，「まあいけそうだ」ということになったようだ。

　下に示した図は，論理加算の具体例だ。これは，入射Aと出射B，入射Cと出射Dという構造を持つ3Dモデルと，入射Eと出射Fという構造を持つ3Dモデルの加算演算を模式図化したものである。

LDC同士の論理加算演算。「入射Aと出射B，入射Cと出射Dという構造を持つ3Dモデル」が上段，「入射Eと出射Fという構造を持つ3Dモデル」が中段で，その加算演算結果が下段となる

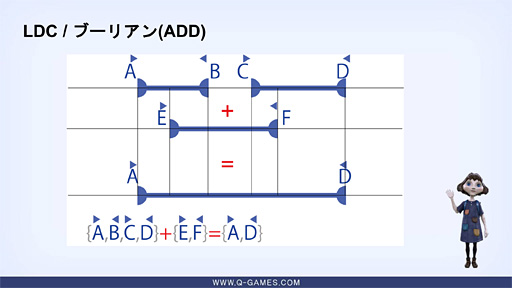　2つの3Dモデルが重なり合う場合，入射Aと入射Eでダブるため，加算の解答候補に入射Aは残す一方，入射Eは除外する。これが論理加算における定義上のルールである。
　続いて出射Bが来るが，入射Eのペアとなる出射Fの登場があるまで，解答候補側への出力をしない。なのでその後，入射Cが登場するが，これも解答候補側への出力はなされない。続く出射Fは，入射Eとのペアなので，論理加算ルールの適用法則が終わる。
　最後に出射Dが登場し，これを解答候補に出力して，結果として出力解答は｛▶A，◀D｝となる。

　……といった具合に，アルゴリズムとしてはいま紹介したとおりなのだが，理屈よりも，模式図を感覚的に理解してもらったほうが早いかもしれない。

　続いては論理減算だ。模式図の見方自体は加算と変わらない。

LDC同士の論理減算演算。見方は同じで，「入射Aと出射B，入射Cと出射Dという構造を持つ3Dモデル」が上段，「入射Eと出射Fという構造を持つ3Dモデル」が中段で，その減算演算結果が下段となる

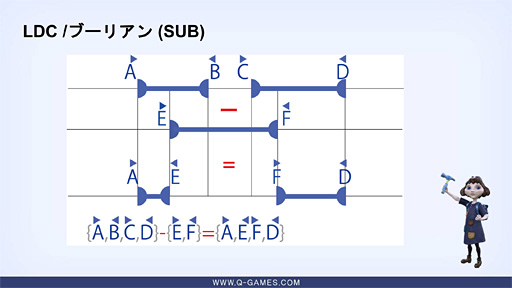　やはり順番に見ていくと，入射Aときて入射Eとくるが，入射と入射でダブっったところで，入射Eは解答側では出射Eとして反転させる。ここが論理減算におけるポイントである。またこの後，出射Bが来るが，入射Eのペアとなる出射Fの登場があるまで解答候補側への出力をしない。このあたりのルールは前出の論理加算と同じだ。なのでその後に登場する入射Cも解答候補側への出力はなされない。

　続く出射Fは，入射Eとのペアなので，論理減算ルールの適用法則が終わる。そのとき，論理加減算のルールとして出射Fを入射Fに反転させて解答側へ出力する。
　最後に登場の出射Dを解答候補に出力して，結果として出力解答は｛▶A，◀E，▶F,◀D｝となる。こちらも図を見れば感覚的に理解できるのではないかと思う。

　なお，ここまで解説してきたのは，あくまでも3Dモデル2個の間におけるジオメトリ情報（＝頂点レベル）の論理加算減算だ。実際には界面形状が変化する（＝2つの3Dモデルで加減算を行えば形状が変わる）ので，法線ベクトルも調整しなければならない。

　論理加算の場合，新しく生成された境界点の法線ベクトルは，2つのLDCポイントにある法線ベクトルのどちらかを残すだけで済むが，論理減算の場合は凹面となるため，ベクトルの符号を反転させる必要がある。

　前出の図解をそのまま流用してこの処理を見ていくと，論理加算の場合は，2つの3Dモデルの合成モデルにおいてそれぞれの材質情報が残ることになる。
　2つの材質の境界点となるのは，論理加算ルール「入射，入射がダブっているとき，その後の出射は消失する」が適用されたポイントだ。一方の論理減算の場合は，論理減算の結果で残存した3Dモデル側の材質情報のみが残る。
　これも下に示した2枚の模式図を見ると，理にかなっているのが理解できるのではないかと思う。

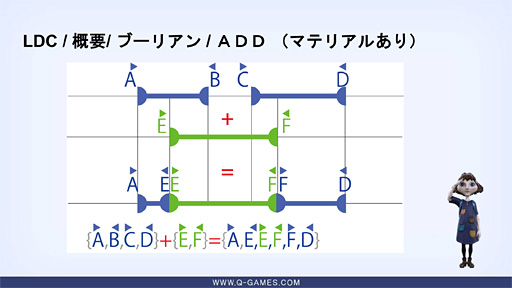論理加算における材質情報（＝マテリアル情報）の残り方。ジオメトリの情報としては｛A，D｝しか残らないものの，マテリアル情報としては｛A，E｝｛E，F｝｛F，D｝が残る

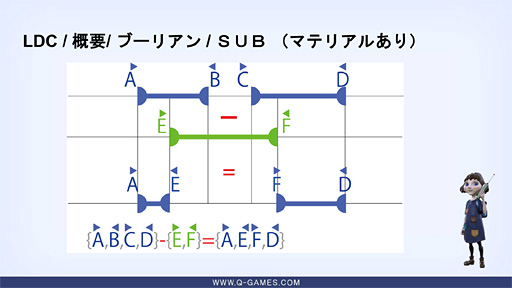論理減算における材質情報（＝マテリアル情報）の残り方。こちらだと，残る材質情報はジオメトリ情報の結果と同じになる

　具体的な3Dモデルを用いた例は以下のとおりだ。

2つの3Dモデルを用いた論理加算の例

2つの3Dモデルを用いた論理減算の例

リアー氏：
　The Tomorrow Childrenでは，ゲーム世界のシステムが作り出す地形はもちろん，ユーザーキャラクターが自ら作り出していく地形もすべてLDCとして持たせています。また地形は，複数の地形部品LDCを論理加算，論理減算で組み合わせたデータになっています。言ってみれば，地形は地形部品の組み合わせで表現されていますから，膨大な地形表現も最低限のデータ量で表現できるんです。
　ゲームシステム上では横1km×縦1km×高さ1kmの範囲の広大なスペースに対して地形の造成が行えますよ。


　ゲーム世界は25.6m×25.6m×25.6mという大きさの立方体「ルートブロック」で区切ってあり，地形部品は，このルートブロック単位で管理されることになる。
　土地の造成は自由に行えるものの「ルートブロックは最大200個」「ポリゴン管理用メモリに限度あり」「LDC格納メモリに限度あり」といった仕様上の制限はあるそうだ。

左のスクリーンショットにおいて，青い線で区切ってある部分がルートブロック。これをさらに軸/面ごとに32×32へ分割したものがLDC Tileだ（右）

　ゲームのシステム管理上，ルートブロックは，描画用の粗い単位である「レンダーセル」（Render Cell）や，より細かい粒度のグリッド「デンスオキュパンシービット」（Dense Occupancy Bit，以下 DOB）に分けられている。

ルートブロック（青）とレンダーセル（緑）

　このあたりはThe Tomorrow Childrenというゲームの都合に依存した実装の話なので，ザックリと解説するが，レンダーセルは描画対象となる地形部品を含むグリッドのことで，単位サイズは6.4m×3.2m×6.4mだ。

レンダーセルを細かく分割したDOBは「LDCデータがある」「ない」の情報を保持している

　DOBとは，レンダーセルを32×16×32で区切ったグリッドで，「LDCデータがあるか/ないか」のフラグ情報を1か0の値で保持するものだ。
　DOBは階層構造になっており，最も精細なのが前述した32×16×32で区切ったもので，このとき一辺は0.2mとなる。一段粗いDOBは一辺が2倍のものというイメージだ。このDOBは主に物理シミュレーション処理で使うことになる。

DOBは「LDCデータがある」「ない」の情報をより高解像度で持つボクセル（≒グリッド）という理解でいい。最も粒度の細かな一辺が20cm幅のもので，一段，粗いサイズのDOBは，一辺サイズが二倍となる。粗いDOBは物理Query(探査)における空間スキップに利用し，衝突などの判定は最も細かい粒度のDOBで判定する

The Tomorrow Childrenの3D地形表現を支える技術（2）デュアルコンターリング法

　さて，地形データはLDCデータとして持てば万事解決かというと，そうでもない。あくまでスタート地点に立ったという感じである。
　というのも，LDCデータのままではGPUによる描画を行えないからだ。あらためて言うまでもないと思うが，PS4のGPUはLDCをレンダリングできない。LDCの集合体として表現される地形をポリゴン化して初めて描画できるようになるのだ。


リアー氏：
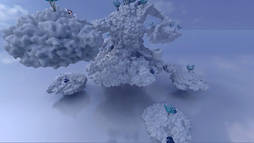
　開発最初は，LDCのポリゴン化にマーチングキューブ（Marching Cube）法を使っていました。しかし，地形部品のディテール消失具合が大きかったり，意図しない凹凸や変形が発生したりして，簡単に言うと品質が低くなってしまうんです。

LDCをマーチングキューブ法でポリゴン化し，レンダリングしたテスト結果

　そこでマーチングキューブ法の採用を断念し，別の方法を模索することになったのですが，その過程で，デュアルコンターリング（Dual Contouring）法が有効だということが分かってきました。LDCという構造体は，基となっているポリゴンモデルの法線ベクトルや頂点データを残してくれているので，ディテールをある程度維持できるのです。

LDCをデュアルコンターリング法でポリゴン化し，レンダリングしたテスト結果

　ちなみに，デュアルコンターリングはCompute Shader（＝GPGPU）で実装しました。


　開発チームがまず不採用としたマーチングキューブ法だが，リアルタイム3Dグラフィックスにおいてしばしば見かけるキーワードなので，ここで軽く紹介しておきたい。

　マーチングキューブ法は，ボクセルなどの単位立方体（＝グリッド）ベースで表現される3Dデータ構造をポリゴン化して可視化するための定番アルゴリズムだ。
　立方体の1頂点に着目すると，（対角側の頂点を除けば）当該頂点と向かい合う頂点は3つある。ここで，ポリゴン化の対象となるグリッドデータを精査して，これら「向かい合う3つの立方体の頂点」間のどこに新しい頂点を打つべきかを計算して求める。この「計算」は取り扱うグリッドデータに応じていろいろで，たとえば流体シミュレーションの結果として気体をポリゴン化して可視化する場合であれば，グリッド値に格納されている密度分布で決めたりする。

　で，この「新たに打った3つの頂点」を結べば，当然のことながら三角形ができる。
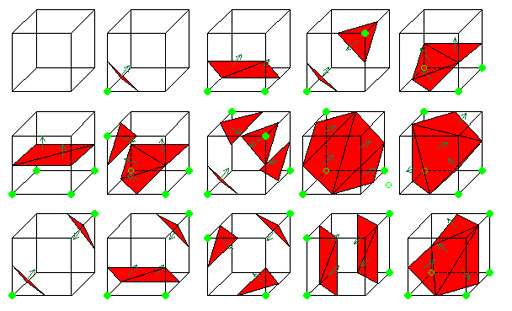
　立方体の場合，頂点は8つあるので，この三角形の生成バリエーションは2の8乗，すなわち256通りある。しかし，回転や反転で表現できるものを重複と考えて排除すれば，固有バリエーションは15通りとして考えることができる。この15種類の「ポリゴンの打ち方」を組み合わせて，表現対象のグリッドデータをポリゴン化していくわけだ。

マーチングキューブ法の基本となる「ポリゴンの打ち方」15種類。1つの立方体で複数のポリゴンが出てくるのは，隣接するグリッドの頂点間で生成されるポリゴンについての組み合わせにも配慮するため。立方体の向かい合う8個の頂点間に任意の頂点を打ったときに生成されるポリゴンの，生成のされ方の全パターンを示したのがこの図である
出典：マーチングキューブのアルゴリズムを解説したサイト「THE MARCHING CUBES」

頂点が複数打たれたときに「どうポリゴンを生成するか」の判断に，幾つかの候補が浮上する場合がある。その判断に誤るとそこで形状エラーが出てしまうのがマーチングキューブ法の弱点。この図はマーチングキューブ法を二次元で見せたときの悪条件の例だ
出典：マーチングキューブのアルゴリズムを解説したサイト「THE MARCHING CUBES」

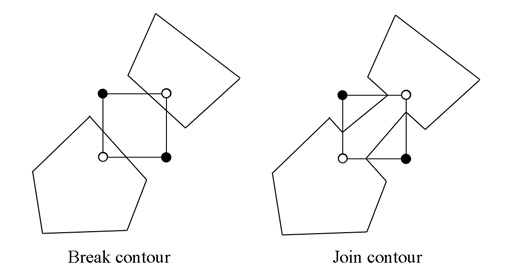　先ほど例示もしたとおり，マーチングキューブ法は，複数の頂点が打たれたときのポリゴン生成が本来の形状とは異なってしまった場合，表現品質が下がってしまう。そこで開発チームはデュアルコンターリング法を採用したということなのだが，こちらも基本的なアルゴリズムはシンプルなものである。

　LDCデータに含まれる点情報「LDC Point」には，座標値に相当する距離データ以外に法線ベクトルも含まれている。そこで，LDCの単位グリッドにおけるX，Y，Z軸各基準面から，LDC Pointの法線ベクトルに対して直交する方向へ面を展開し合い，それら面同士から最も近い位置をポリゴンの頂点として生成するのだ。

　これも，二次元へ次元を下げて図解するとアルゴリズムが理解しやすい。
　下の図はマスがLDCの単位グリッド，青軸がそのX軸，赤軸がY軸。茶色の部分がLDC Pointから再現される形状をそれぞれ示している。ここで青点をX軸のLDC Point，赤点をY軸のLDC Pointとしたとき，各軸のLDC Pointから法線ベクトルと直交する部分へ線分を延長して，その交差点を「ポリゴン化に用いる頂点」とするのである。
　生成した頂点のことを開発チーム内では「Dual Contuoring Vertex」（デュアルコンターリングバーテックス，以下，DC Vertex）と呼んでいたという。

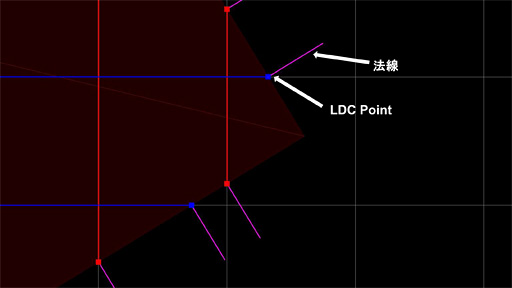二次元でDual Contouring法を考えてみたところ。「法線」が法線の方向（＝法線ベクトル）だ

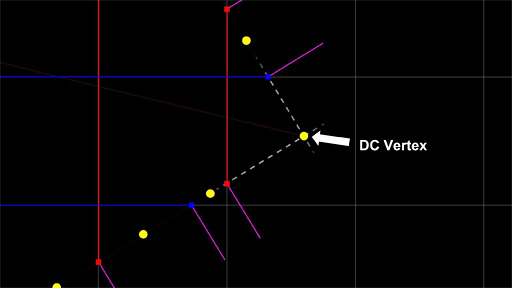LDCデータのLDC Pointから「ポリゴン化に用いる頂点」を求めるアルゴリズムのイメージ

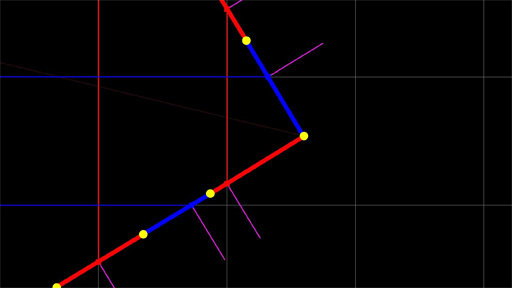生成したDC Vertexを結ぶと線分ができあがる

　DC Vertexは，LDC単位グリッドあたり1個生成されるので，隣接する単位グリッドのDC Vertex同士を線分で結ぶと，四辺形ができあがる。
　そう，ここまで「ポリゴン化」という言葉を使ってきたが，LDCデータからデュアルコンターリング法を用いて生成することになるポリゴンは，三辺形ではなく四辺形（＝三辺形2枚，専門用語で言う「クアッド」（Quad））のポリゴンになるのである。

ここまで二次元で語ってきたが，こちらは三次元に拡張したイメージ。DC Vertexを結ぶ線分は三次元的なものになる。ここで中央に見える赤い線分がLDC単位グリッドを構成するものの1つで，そこに打ってある水色の点がLDC Point。ここを基準にして求めることのできるDC Vertexは隣接する4つのLDC単位グリッド内に生成されるので，これらを結べば四辺形になるわけである

実際に，どんな感じで地形が四辺形ポリゴン化されるのか示したイメージ

リアー氏：
　マーチングキューブ法と違い，デュアルコンターリング法による結果だとポリゴンエッジが鋭く，不自然なノイズチックな凹凸も少ないという，おおむね満足できる結果が得られました。
　しかし，2つの異なる材質表現（＝マテリアルID）が付随した地形部品モデルを組み合わせて造成したときには，その2つの地形部品モデルが重なったところに，ギザギザとした材質表現の境界線ができてしまうことがあり，これが気になったのも確かです。

デュアルコンターリング法で実装した，側面と上面で材質表現の異なる岩。境界付近に注目すると，ギザギザした境界線が出ているのが分かる

　この問題に対しては，隣接する頂点同士を平均化することで，ギザギザ感を低減させるハック（※根本解決ではなく，その場しのぎ的な個別対策）を適用して解決したそうだ。

隣接する頂点を平均化することでギザギサ感を低減。高周波のディテールは低減してしまうが，滑らかさのほうを優先させたという

リアー氏：
　今回用いたLDCのような，均等な距離区切り（≒グリッド）で表現したデータ構造の場合，デュアルコンターリング法でポリゴン化したときに，精度の問題で穴や割れ目ができてしまうことがありました。そうした問題に対しては，個別のハックで対応していますね。たとえば，DC Vertexの生成を，着目している部分の少し外側にあるLDCの単位グリッドに対しても行うようにする，といった対応です。

上下段とも左側が穴あき現象ありのスクリーンショット。輝いて見える破れ目のようなところが，デュアルコンターリング法による「LDC→ポリゴン化」の精度不足で生じた「穴」だ。右側が対策後のスクリーンショットで，見事に「穴」が消えているのが分かる

The Tomorrow Childrenの3D地形表現を支える技術（3）実際の地形描画

　ここまでの流れを，おさらいとして一度振り返っておこう。
　The Tomorrow Childrenでは，「盛ったり掘ったり」を実現できるような，自在な土地造成をユーザーレベルで行えるよう，土地部品を積層させる仕組みを導入することにした。
　それにあたり，3Dモデル（＝土地部品）同士の論理演算を行うのに効率のいい，ポイントクラウド的なLDCという概念を導入。ただこのままだとGPUによる描画を行えないため，デュアルコンターリング法によってポリゴン化することにした。

　以上を踏まえてここからは，「ポリゴン化された地形を，いかにして実際の描画プロセスへ落とし込むのか」を見ていきたい。
　The Tomorrow Childrenが，ボクセルコーントレーシング（Voxel Cone Tracing，以下，VCT）ベースの描画パイプラインを採用してリアルタイム大局照明（Real-time Global Illumination）を実装していること，そしてその根幹部分にはG-Buffer（＝中間パラメータを収納する画面解像度と同解像度での作業バッファ）を活用したディファードレンダリング（Deferred Rendering）があることは前編で解説したとおりだ。

　ポリゴン化された地形も当然，この描画パイプラインを使って描画することになる。
　地形が地形部品の組み合わせによって構成されていることは本稿で説明してきたとおり。各地形部品に付随する材質情報（＝マテリアルID）は「できあがっている地形」に継承されるので，地形がディファードレンダリングの前段パスであるジオメトリレンダリングを通ると，地形の材質情報もちゃんとG-Bufferに反映されることになる。
　具体的にはアルベド（Albedo，入射光と反射光の比。実質的には拡散反射項），スペキュラ（Specular，鏡面反射項），表面下散乱量，マテリアルID（材質属性）などがピクセル単位でG-Bufferへ出力されるのだ。

The Tomorrow Childrenでは，地形部品ごとにさまざまなな材質属性が与えられている。これは，地形部品がクリスタル状の半透明な材質である例

地形部品ごとの材質情報はゲーム進行に合わせ，ポリゴン単位でリアルタイムに変更することも可能。画面は青っぽい氷の岩壁の一部を苔のような材質に変更した例だ

地形部品の材質情報には，ポリゴン化の際に追加の凹凸を与えられる要素「Displacement」（ディスプレースメント）を盛り込むこともできる。左上は標準状態。右上は低周波のパーリンノイズで揺らいだ変移を与えた状態で，雲のように見える。左下は高周波のパーリンノイズで揺らぎを与えた状態で，トゲトゲの荒々しい岩盤のように見える。右下は煉瓦状のカクカクした変移を与えた状態で，こちらだと人工的な加工がなされたように見える

リアー氏：
　地形には一般的なテクスチャリング手法である「一意的なUVマッピング」が利用できません。というのも，仮にLDCにUV情報を入れ込んだとしても，デュアルコンターリング法による「LDC→ポリゴン化」のときに失われてしまうからです。
　そこでThe Tomorrow Childrenでは，地形へのテクスチャリングに「トライプレーナテクスチャリング」（Tri-Planer Texturing）を使っています。


　トライプレーナテクスチャリングというキーワードについても解説が必要かもしれない。

　これは凹凸表現が豊富なテクスチャリングにおいてよく使われる定番手法の1つだ。
　テクスチャの貼り付けでは，「平面画像としてのテクスチャ」と「起伏を含むポリゴンの集合体（＝3Dモデル）」との対応付けを設計しておくのが一般的だ。これが「UVマッピング」であり，GPU上では，与えられたUV情報から，「ポリゴンから見た，テクスチャマップの対応」を決定している。ハードウェアレベルで言えば，テクスチャメモリのアドレス指定を決めているわけである。
　ただし，UVマッピングの場合，凹凸が強すぎる地形表現を前にすると，下のような結果となってしまう。

UVは平面に「ポリゴンから見た，テクスチャマップの対応」が定義されるので，起伏が激しくなりすぎるとテクスチャが間延びしてしまう
出典：Brent Owens氏，「Use Tri-Planar Texture Mapping for Better Terrain」

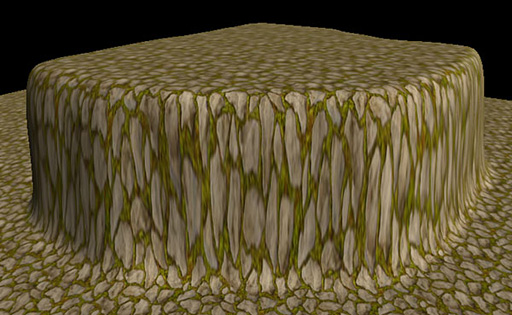　こうした現象を低減するために生まれたのがトライプレーナテクスチャリングという技術で，イメージとしては，現実世界でプロジェクタからプロジェクションマッピングを行うように，3方向からテクスチャリングを行うものとなっている。
　この「3方向」は，テクスチャ適用先のポリゴンに対するX，Y，Z軸のことを意味している。よくよく考えると，トライプレーナテクスチャリングの「Tri-Planar」は「3平面の」という意味なので，本技法はその名前がほぼそのままアルゴリズムを表しているのだった。

トライプレーナテクスチャリングは，3方向からの投射テクスチャマッピングを実現する技法
出典：Brent Owens氏，「Use Tri-Planar Texture Mapping for Better Terrain」

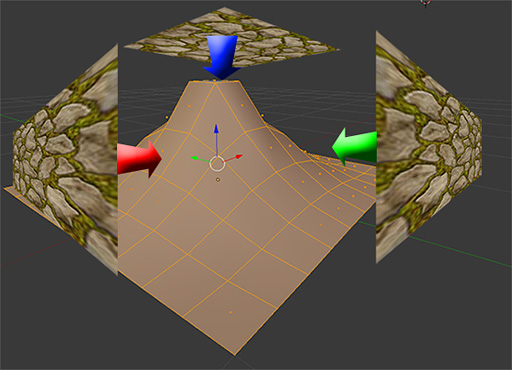　たとえば，適用先となるポリゴンの傾き具合がX軸に対して80％の角度で相対していて，Z軸に対して20％の角度で相対していたとすれば，X軸から投射させるテクスチャ適用率は80％，Z軸から投射させるテクスチャ適用率は20％としてブレンドさせる。
　すると，下に示したスクリーンショットのように，UVマッピングベースで得られた，間延びしたテクスチャと比べると，相当マシな結果が得られる。テクスチャ岩肌や模様，鱗（うろこ）といった完全な反復パターンの場合だと，X，Y，Z軸から適用したテクスチャをブレンドしたときに生じる境界の違和感は目立たない。よほど近づいてあらを探さなければ気がつかないだろう。

トライプレーナテクスチャリングを適用した例。UVベースのテクスチャマッピングと比べるとかなりマシだ
出典：Brent Owens氏，「Use Tri-Planar Texture Mapping for Better Terrain」

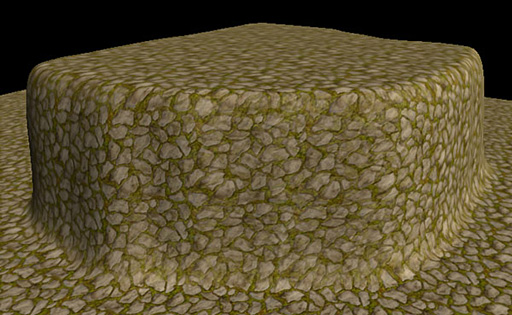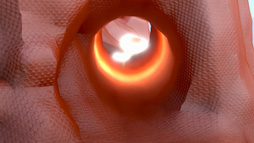
　The Tomorrow Childrenでは，地形に対してこのトライプレーナテクスチャリング技法を用い，微細な凹凸表現用の法線マップも含めたテクスチャを適用している。実際に，このテクニックを適用した分かりやすい事例が下のスクリーンショットだ。

トライプレーナテクスチャリング技法を使った事例。岩肌は不規則な凹凸模様，トンネルは規則的なハニカム状の凹凸模様となっているが，これはX，Y，Z軸から投射するテクスチャの種類を個別に設定することで実現している

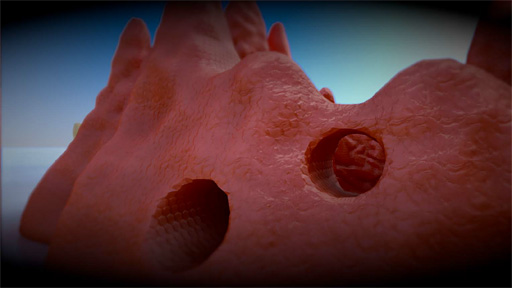　さて，広大なゲームフィールドが舞台となるThe Tomorrow Childrenで，地形描画時のLoD（Level of Detail）処理はどうなっているのだろう（※キャラクターモデルにおけるLoD処理は前編で紹介済みだ）。
　LoD処理とは，描画する3Dモデルの頂点数を視点からの遠近に応じて増減させる仕組みのことで，近距離にあるオブジェクトは多くのポリゴンで，遠距離にあるオブジェクトは少ないポリゴンで描画することにより，描画品質と付加とのバランスを取る技術である。


リアー氏：
　地形のLoD処理は3レベルで適用しています。とてもシンプルな実装で「LDC→ポリゴン化」にあたり，視点からの距離に応じてポリゴン化粒度の増減を行うというものです。GPU側のテッセレーションステージなどは使っていません。


　The Tomorrow Childrenでゲーム世界の地形を一辺20cmのLDC単位グリッドで表現するというのはここまで繰り返し述べてきたとおりだ。これを描画する前段階でポリゴン化するわけだが，最も高精細なLoDレベル0の近距離な地形に対しては，この「LDC→ポリゴン化」をLDC単位グリッドの間引きなしで行う。
　そして一段品質の下がるLoDレベル1では，LDC単位グリッドを1つ飛ばしで処理してポリゴン化する。換言すれば地形のポリゴン化精度は一辺40cm精度まで下げるということだ。同様にLoDレベル2では，レベル1の状態からさらに1つ飛ばしして，ポリゴン化の精度をさらに半分に落とすことになる。

　なお，LoDレベル0はプレイヤー視点から40mの範囲内で適用され，その先，125mまでがLoDレベル1の範囲となる。その先はすべてLoDレベル2だ。
　ただし，ゲーム世界を覆っている異物「ボイド」の中では全体がぼやけた表現になるため，LoDレベル0は使われない。プレイヤー視点から15mの範囲まででLoDレベル1，それより先では280mまでLoDレベル2を使うという。なら280mより先は？　というと，そこは「見えない」として描画しないとのことである。



リアー氏：
　LoDレベル1以降の低精度表現では，LDC単位グリッドを飛ばしてポリゴン化するので，ポリゴン化された3Dモデルにはエイリアシングが出て，品質がかなり下がります。それこそポッピングが起きやすくなるレベルです。
　この表現劣化をプレイヤーに見せたくないので，こうした表現劣化が隠蔽できるほどの遠方からLoDレベル1以降を利用するような制御にしています。


　そういえば，地形が出現したり消失したりする，あの美しいアニメーションはどのように実現されているのだろうか。


リアー氏：
　The Tomorrow Childrenの地形は，LDC単位グリッドから「LDC→ポリゴン化」処理でポリゴン化しているので，地形モデルは均等サイズのポリゴンで表現することになります。ですので，地形を構成しているポリゴンをそのままパーティクルとして扱って飛ばすことであのアニメーションを実現しているんです。


　なるほど，あの表現は一種のプロシージャルアニメーションなのだ。
　消失アニメーションでは，各ポリゴンは時間経過と共に小さくなって消えていき，出現アニメーションでは逆になるとのこと。また，各ポリゴンの隙間を隠しつつ，ポリゴンの三角形としての形を隠蔽するため，各頂点にセルノイズの変移を与える工夫も盛り込んであるという。

「他が試みていない技術」がてんこ盛りのThe Tomorrow Children

　本連載では最長となる，前・中・後の3回にわたってお届けしたThe Tomorrow Childrenも今回で終了となる。
　実のところ本作では，AIや物理の話題もかなり面白そうなのだが，本連載はあくまでもグラフィックスをテーマにしたものということで，ひとまずこのあたりで締めくくらせてもらえればと思う。

　難解な部分も多かった，というか，人によっては全編にわたって難解だったのではないかと思うが，それだけThe Tomorrow Childrenは，他が試みていないアプローチのグラフィックス技術を多用しているということである。後の作品に少なからず影響を及ぼしていくものになるのではないかと，筆者は考えている。

　また，ここまで読み進めて，ゲーム本編にも興味を示してもらえたなら幸いだ。

西川善司の「試験に出るゲームグラフィックス」（4）レイトレアプローチで作り上げたThe Tomorrow Childrenの先進ビジュアル，前編

西川善司の「試験に出るゲームグラフィックス」（5）レイトレアプローチで作り上げたThe Tomorrow Childrenの先進ビジュアル，中編

PlayStation.comのThe Tomorrow Children公式ページ

キュー・ゲームス公式Webサイト