ニュース
円周率の小数点以下8000兆桁めをGeForceで求める方法〜GTC 2013の「π」セッションレポート
 |
| Ed Karrels氏 |
 |
| セッションタイトル |
しかもその計算をCPUではなく,ましてはHPC(High Performance Computing)向けGPUであるTeslaでもなく,ごくごく一般的なGeForce製品で達成したというのだから驚きだ。
GPU Technology Conference 2013(GTC 2013)では,本研究グループのリーダーであるEd Karrels氏によるセッション「Computing the Quadrillionth Digit of Pi: A Supercomputer in the Garage」(円周率の千兆桁めを求める:ガレージのスパコンで)が開かれたので,レポートしよう。
円周率の小数点以下8000兆桁めを
自作PCで求めた大学院生
一般に円周率の計算の記録というと,3.1415926535…と頭の桁から順番に求めていく桁数や速度をイメージする人が多いのではないかと思う。
この方式の計算記録としては,2011年に,長野県在住の会社員・近藤 茂氏と米国で当時大学院生だったAlexander J.Yee氏とが共同で達成した「自作PCで1年間かけて計算した10進法10兆桁」がある。
 |
 |
 |
冒頭で8000兆桁めと述べたとおり,Karrels氏らが達成したのは,このYahoo!の記録を上回る,2進法8000兆桁めからの算出記録だ。
Yahoo!の研究チームは,8コアCPUベースのコンピュータ1000台で23日かけて2000兆桁めを求めた。それに対してKarrels氏らは,わずか4基のGPUを搭載しただけの自作PCで,24日間で2000兆桁めに到達。計算速度ではYahoo!の記録を破れなかったが,確かな手応えを感じた氏らは,続いて小数点以下4000兆桁めの計算に挑戦し,37日間で目標を達成したとのことだ。
そして最後に8000兆桁めの計算に挑戦するわけだが,ここではハードウェアを増強し,大学の計算機室にあったPCまでも総動員して臨んだという。結果,26台のPC,総GPU数にして34基――下のスライドには「30 GPUs」とあるが,これはグラフィックスカードの枚数とのこと――を駆使し,26日間でこの記録を達成したのだった。
 |
円周率の小数点以下N桁めからD桁分を求める方法
 |
そこで,計算の途中に剰余を算出する計算である「mod」を介入させる。
この計算に都合がいいのが,David H.Bailey氏とPeter Borwein氏,Simon Plouffe氏,米国とカナダの数学者による合同チームが1995年に考案した「Bailey-Borwein-Plouffeの公式」(以下,BBPの公式)というアルゴリズムである。
 |
 |
 |
BBPの公式アルゴリズムで示される無限級数では,「16のk乗分の1」が頭に出ていることから,16進数でのN桁めを得たい場合には,16のN乗を各項に掛けてやれば,簡単にN桁めを小数点のところに持ってくることができる。また,この無限級数に16のN乗を掛けて変形すると,各項の分子項は2のべき乗で表せるようになる。そうなれば,高速に計算が可能だ。付け加えると,各項の計算は独立しているので,並列に計算できる。
 |
| BBPの公式の各項に16のN乗を掛けてやれば,小数点以下N桁めからが求まるではないか。ただし16進数表記にはなるが |
 |
| 小数点以下を求める計算「fract」の意味を理解してみよう |
 |
| 根幹計算を高速化するには? |
 |
そこでKarrels氏らは,BBPの公式の別バリエーションである「Bellardの公式」を採用し,なおかつmod計算をビット操作だけで済ませられるように「モンゴメリ乗算」(Montgomery Reduction)のアルゴリズムを取り入れてmod演算部分の高速化を実現したという。
 |
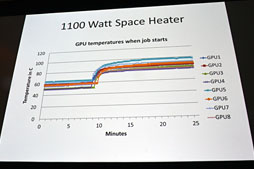
時代はゲリラ・スーパーコンピューティングへ!?
 |
 |
 |
 |
ところで,今回の計算実行にあたって,計算器室に置かれたコンピュータの大部分を円周率計算で占有すると,さすがに顰蹙(ひんしゅく)を買ってしまうため,「誰かがログインしたら,当該PCで円周率計算実行をアイドルさせる」制御を入れたそうだ。まるで,ウイルスかマルウェアのような振る舞いだが,Karrels氏いわく,「これこそが新しいスーパーコンピューティングの形,『ゲリラ・スーパーコンピューティング』だ(笑)」とのことである。
 |
- 関連タイトル:
 GeForce GTX 600
GeForce GTX 600 - 関連タイトル:
 GeForce GTX 500
GeForce GTX 500 - この記事のURL:
キーワード
- HARDWARE:GeForce GTX 600
- GPU
- GeForce
- NVIDIA
- HARDWARE:GeForce GTX 500
- HARDWARE
- GPU Technology Conference
- ニュース
- イベント
- ライター:西川善司
Copyright(C)2010 NVIDIA Corporation